Учёные из Университета Лобачевского создали достаточно точную математическую модель социальных конфликтов

Группа исследователей под руководством профессора Александра Петухова из Института международных отношений разрабатывает модели социальных конфликтов на базе методов нелинейной динамики.

Для математического моделирования важным свойством общественных и политических процессов является невозможность их строгого определения. Они всегда подвержены небольшим изменениям и флуктуациям. Часто общественные процессы сравнивают с броуновскими частицами. Небольшие изменения (флуктуации) их траекторий объясняются хаотически движением других молекул. В социальных процессах флуктуации можно рассматривать как результат проявление свободной воли отдельных участников, а также как следствие случайных воздействий окружающей среды.

Подпись к изображению: Фазовая траектория социальной системы в конфликтной ситуации в отсутствии внешнего воздействия

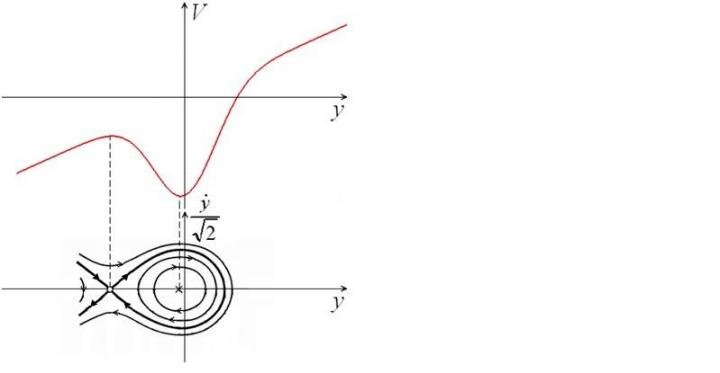
В физике эти процессы обычно описывают уравнением стохастической диффузии Лангевина, которое также было использовано в моделировании некоторых общественных процессов.

Основанный на этих уравнениях подход имеет определённые преимущества:

1. Как уже упоминалось, он позволяет принять во внимание проявления свободной воли отдельных участников, а также и другие случайные воздействия окружающей среды, внешней по отношению к социальной системе.
2. Поведение социальной системы можно рассчитать как для системы в целом, так и для её индивидуальных элементов.
3. Этот подход позволяет идентифицировать некоторые характерные устойчивые режимы функционирования социальной системы, зависящие от разных начальных условий.
4. Уравнения диффузии как математический инструмент достаточно проверены и подтверждены для использования в численном моделировании.

Рассматриваемая модель основана на предпосылке, что в обществе индивиды взаимодействуют через коммуникационное поле h. Это поле, создаваемое каждым индивидом в обществе, формирует информационное взаимодействие между ними.

Однако следует понимать, что здесь мы говорим об обществе как об объекте, который всё же не является объектом в привычном физическом смысле.

По словам доктора Петухова, с точки зрения передачи информации между индивидуумами, пространство сообщества объединяет классические пространственные координаты и дополнительные, специфичные характеристики. Это объясняется тем фактом, что в современном информационном мире нет необходимости находиться физически близко к объекту воздействия для передачи ему информации.

«Таким образом, общество многомерно, а социальное и физическое пространство отражают способность индивида «достать» до другого своим коммуникационным полем, то есть повлиять на другого индивида, его параметры и на способность перемещаться в данном пространстве», — отметил Александр Петухов.

Соответственно, положение индивида относительно других в таком пространстве предоставляет модель уровня их взаимоотношений и степени их вовлечённости в информационный обмен. Когда индивиды находятся близко друг к другу в этой модели, это означает наличие регулярного обмена информацией между ними и то, что социальный контакт установлен. Если же некое взаимодействие между индивидами или их группами приводит к резкому росту расстояний — это означает конфликт.

Следовательно, уподобляя индивида броуновской частице с определённым радиусом влияния на других индивидов, коммуникационное поле можно представить, используя уравнение диффузии.

Основываясь на представленном выше подходе и на модели, созданной исследователями из Университета Лобачевского, учёные обнаружили следующие характерные паттерны и зависимости для начальных и граничных условий:

1. Были установлены граничные условия, с учётом внешнего воздействия, при которых появляются основания для возникновения общественного конфликта и его эскалации. Такие условия определяются параметрами социальной системы.
2. Была найдена характерная область устойчивости социальной системы. В этой области, определяемой фазовыми траекториями, относительно небольшое социальное расстояние остаётся постоянным. Эта ситуация характерна для активно взаимодействующих групп населения, поддерживающих непрерывный информационный контакт. В то же время было отмечено то, как меняется эта область в зависимости от воздействия функции управления конфликтом.
3. Определив и связав между собой эти граничные состояния, при введении параметризации функции управления, стало возможным определить паттерны, соответствующие конкретным современным этнико-социальным конфликтам. Таким образом, эта модель может быть использована как инструмент предсказания динамики конфликта, и для выработки сценария его урегулирования.

Также в ходе исследования было показано, что переход распределённой мультикомпонентной когнитивной системы из устойчивого состояния в неустойчивое является пороговым эффектом. Согласно Петухову, проведённые в Университете Лобачевского эксперименты выявили специфичные параметры, необходимые для контроля над такой системой: они определяют переход из устойчивого состояния в неустойчивое, что даёт возможность (при наличии полного контроля над этими параметрами) создать условия для проявления социального конфликта, или, наоборот, предотвратить его.

«Развивая этот подход, в будущем мы сможем на его основе создать полноценный инструмент предсказания общественных конфликтов», — подытожил Александр Петухов.

Источник

02.07.2018 13:30